Halina Jabłońska
Irena Słowikowska
Gimnazjum w Szydłowie
Program nauczania: Matematyka z plusem nr DKW – 4014-139/99
Temat: Zapisywanie i odczytywanie wyrażeń algebraicznych.
Czas trwania zajęć: 2 x 45 minut
Cele
dydaktyczne:
a) szczegółowe – uczeń potrafi:
- nazywać wyrażenia zapisane za pomocą symboli matematycznych,
- zapisywać za pomocą symboli matematycznych wyrażenia przedstawione słownie,
- stosować kolejność działań,
- stosować zasadę dziesiątkowego systemu pozycyjnego,
- stosować pojęcia: dzielnik, wielokrotność, liczba parzysta, liczba nieparzysta,
b) uniwersalne – uczeń doskonali umiejętności:
- wiązania arytmetyki z algebrą,
- posługiwania się językiem matematycznym,
- stosowania uogólnień i analogii,
- współpracy i komunikowania się w grupie.
Metody i
techniki pracy:
- podająca,
- eksponująca,
- praktyczna.
Formy
organizacyjne:
- praca z całą klasą,
- praca w grupach,
- praca indywidualna.
Pomoce
dydaktyczne:
- gra dydaktyczna - domino,
- kartki z zadaniami,
- podręcznik,
- tablica, kreda.
Typ lekcji: wprowadzająco – ćwiczeniowa.
Literatura:
1. Dubiecka A., Gaweł M., Igraszki z matematyką., Wydawnictwo NOWIK, Opole 1996.
2. Łęska W., Łęski S., I ty zostaniesz Pitagorasem. Materiały pomocnicze do nauki matematyki dla klasy 7., Oficyna Wydawniczo-Poligraficzna „ADAM”, Warszawa 1997.
3. Praca zbiorowa pod redakcją M. Dobrowolskiej, Matematyka 1. Podręcznik dla klasy pierwszej gimnazjum., Gdańskie Wydawnictwo Oświatowe, Gdańsk 1999.
4. Treliński G., Wachnicki E., Matematyka. Podręcznik dla klasy siódmej szkoły podstawowej., WSiP, Warszawa 1990.
I.
Czynności organizacyjne i sprawdzenie pracy domowej
II.
Część wstępna
1. Podanie tematu i objaśnienie celów lekcji.
2. Przypomnienie znaczenia pojęć: wyrażenie algebraiczne, suma, różnica, iloczyn, iloraz, dzielnik, wielokrotność.
3. Rozdanie kartek z zadaniami do pracy indywidualnej (zadania: nr 1 i nr 2 – Załącznik nr 1).
4. Praca samodzielna uczniów – rozwiązanie zadania nr 1. Po zakończeniu pracy, rozwiązania są omawiane wspólnie.
III.
Część zasadnicza
1. Omówienie zasady nazywania wyrażeń algebraicznych na przykładach:
a) suma
![]()
b) różnica
![]()
c) iloczyn
![]()
d) iloraz
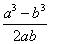
2. Praca samodzielna uczniów – rozwiązanie zadania nr 2. Po zakończeniu pracy, rozwiązania są omawiane wspólnie.
3. Podział klasy na czteroosobowe grupy o zróżnicowanym poziomie.
4. Rozdanie kartek z zadaniem nr 3 (Załącznik nr 2) oraz omówienie zamieszczonego na kartkach przykładu. Uczniowie otrzymują kartki z narysowanymi grafami, które należy uzupełnić. Wyróżniony graf stanowi klucz do utworzenia grupy eksperckiej.
5. Podział klasy na grupy eksperckie. Uczniowie przechodzą do grup eksperckich (roboczych) utworzonych według podanego klucza.
6. Praca w grupach eksperckich – uzupełnienie wyróżnionego grafu.
7. Praca w grupach podstawowych. Po zapisaniu wyrażenia i określeniu jego nazwy uczniowie wracają do grup podstawowych i uczą kolegów, w jaki sposób należało uzupełnić dany graf.
8. Kompletowanie rozwiązań. Uczniowie w grupach podstawowych kompletują zadania.
9. Omówienie rozwiązań. Przedstawiciel jednej z grup zapisuje otrzymane wyrażenia na tablicy i podaje ich nazwy.
10. Praca w grupach podstawowych. W tych samych grupach uczniowie rozwiązują kolejne zadanie, którego treść podaje nauczyciel.
Zadanie nr 4
Narysuj grafy dla podanych wyrażeń algebraicznych:
a)
![]()
b)
![]()
c)
![]()
d)
![]()
11. Omówienie rozwiązań. Przedstawiciele czterech grup prezentują kolejne grafy (każdy po jednym przykładzie).
12. Praca z całą klasą.
Zadanie nr 5
Zapisz w postaci wyrażeń algebraicznych:
a) podwojony iloczyn liczb a i b,
b) sumę liczby x i sześcianu liczby y,
c) różnicę kwadratu liczby m. I liczby 5,
d) iloraz trzeciej potęgi liczby a przez różnicę liczb a i b,
e) sześcian sumy pięciokrotności liczby x i połowy liczby y,
f) różnicę ilorazu sumy liczb x i 5 przez liczbę y oraz iloczynu liczb x i y.
13. Rozdanie kompletu 16 kostek domina (Załącznik nr 3).
14. Praca w grupach podstawowych. Uczniowie rozpoczynają grę, wybierając dowolną kostkę. Połączenie się kostek: pierwszej i ostatniej potwierdza poprawność rozwiązania.
15. Praca z całą klasą.
Zadanie nr 7
Niech n oznacza liczbę naturalną. Napisz:
a) trzy kolejne liczby naturalne następujące po liczbie n,
b) liczbę parzystą,
c) liczbę nieparzystą,
d) liczbę podzielną przez 6,
e) liczbę, która w wyniku dzielenia przez 8 daje resztę 7,
f) liczbę, która jest wielokrotnością liczby 23,
g) sumę odwrotności dwóch kolejnych liczb naturalnych następujących po liczbie n,
h) sumę trzech kolejnych liczb parzystych, z których pierwszą jest 2n.
Zadanie nr 8
Zapisz w postaci wyrażeń algebraicznych:
a) liczbę dwucyfrową, w której x oznacz cyfrę dziesiątek, a y cyfrę jedności;
b) liczbę trzycyfrową, w której p jest cyfrą jedności, cyfra dziesiątek jest o 2 większa od cyfry jedności, a cyfra setek stanowi połowę cyfry dziesiątek;
c) liczbę czterocyfrową, w której cyfrą jedności jest x, cyfrą tysięcy jest y, a cyfry setek i dziesiątek są zerami.
1. Rozdanie kartek z zadaniem nr 9 (Załącznik nr 4).
2. Praca w grupach podstawowych. W tych samych grupach uczniowie rozwiązują podane zadanie oraz sprawdzają poprawność rozwiązania według otrzymanego hasła: „MIŁEGO DNIA”.
3. Omówienie pracy grup.
Dla wszystkich uczniów: zadanie 4 str. 146; zadanie 5 a, b, c str. 146; zadanie 14 a, b, c str. 147.
Dla uczniów zainteresowanych: zadanie 5 d, e str. 146; zadanie 14 d str. 147.
Zadanie nr 1
Wpisz odpowiednie wyrażenia algebraiczne:
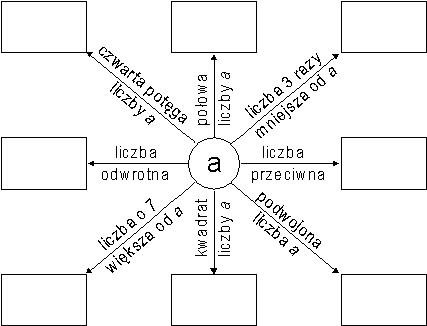 |
Zadanie nr 2
Podane wyrażenia połącz z odpowiednimi nazwami:
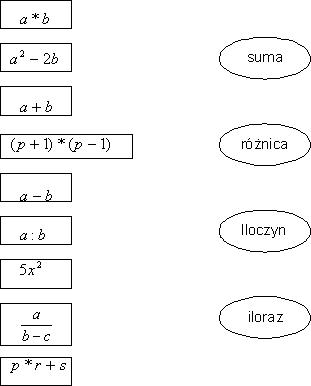 |
|||
|
|||
Załącznik nr 2
Zadanie nr 3
Uzupełnij grafy wyrażeń algebraicznych zgodnie z podanym wzorem:
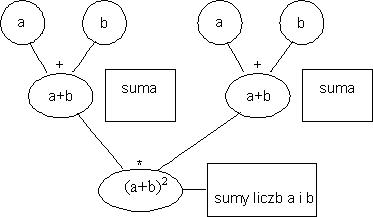 |
Wzór:
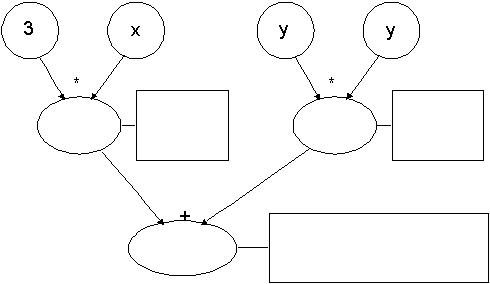 a)
a)
b)
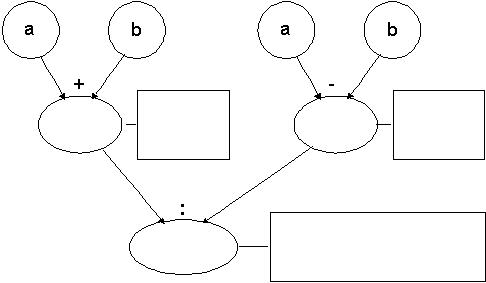 |
c)
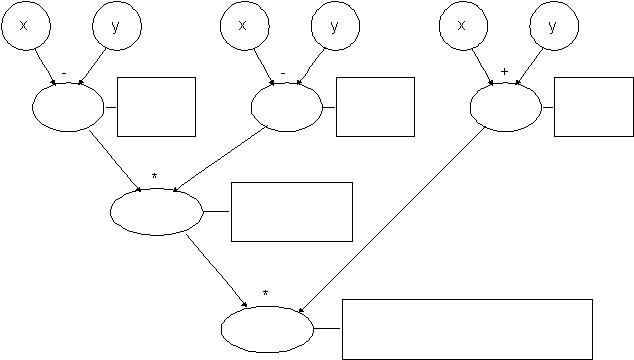
d)
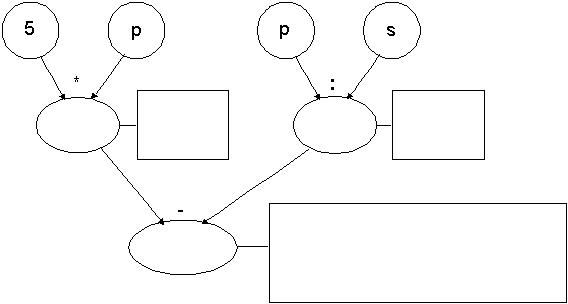
Zadanie nr 6: Domino
| Iloczyn
sumy liczb x i y przez różnicę liczb x
i y. |
|
|
Podwojony
kwadrat różnicy liczb x i y. |
|
| |
|
|
|
|
| Iloraz
pięciokrotności liczby x przez różnicę
kwadratów liczb x i y. |
|
|
Suma
liczby x i trzykrotności liczby y. |
|
| |
|
|
|
|
| Liczba
5 razy mniejsza od sześcianu liczby x. |
|
|
Suma
kwadratów liczb x i y. |
|
| |
|
|
|
|
| Różnica
podwojonego kwadratu liczby y i kwadratu liczby
x. |
|
|
Kwadrat
sumy liczb x i y. |
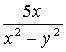 |
| |
|
|
|
|
| Różnica
sześcianu liczby x i czterokrotności liczby y. |
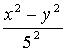 |
|
Liczba
o 5 mniejsza od sześcianu liczby x. |
|
| |
|
|
|
|
| Iloraz
różnicy kwadratów liczb x i y przez
kwadrat liczby 5 |
|
|
Liczba
o 3 większa od x. |
|
| |
|
|
|
|
| Liczba
3 razy większa od x. |
|
|
Trzykrotność
kwadratu sumy iloczynów liczb 3 i x oraz
liczb 5 i y. |
|
| |
|
|
|
|
| Iloraz
sumy liczb x i y przez liczbę 5. |
|
|
Średnia
arytmetyczna liczby x i sześcianu liczby y. |
|
Załącznik nr 4
Zadanie nr 9
Dopasuj wyrażenie do podanej nazwy. W okienka wpisz odpowiednie litery;
n - dowolna liczba naturalna.
Ł 2n2
G 5(2n+1)
D 7n
J n+4
N 7(2n+1)
O 5n+1
E 3n
M (2n)2
A 4n
| J |
I. Kwadrat liczby parzystej.
II. Połowa liczby nieparzystej.
III. Podwojony kwadrat liczby naturalnej.
IV. Trzykrotność liczby naturalnej.
V. Liczba nieparzysta podzielna przez 5.
VI. Liczba, która przy dzieleniu przez 5 daje resztę 1.
VII. Wielokrotność liczby 7.
VIII. Siedmiokrotność liczby nieparzystej.
IX. Liczba o 4 większa od liczby n.
X. Liczba 4 razy większa od n.
I |
II |
III |
IV |
V |
VI |
|
VII |
VIII |
IX |
X |
| |
|
|
|
|
|
|
|
|
|
|